【前端面经】热乎的小米面经总结

写在前面

春招已至，诸多大厂争相上台，比以往的春招更加热烈些。字节、腾讯都突然扩招，让本来就业形势严峻的2021年，注入一剂强心剂。

小米面试

由于走的是内推，直接跳过笔试进入面试，而面试直接就是手撕代码，泪目...还好小米的手撕不是很难。

首先是进行自我介绍，介绍学校、项目、经历、技能等，balabala的。

小插曲，由于自己本身研究方向是深度学习与图像处理，有过前端、后端等开发经验，面试官让我介绍自己的前端学习经历、为什么选择前端。此时脑子一热balabala说了一大堆，面试官直接让我三句话精炼描述下自己的经历，这里非常感谢面试官给我提出了很好的建议，最后回答的是：比较喜欢和擅长前端。

常规题

1. 说下原型链继承和原型链？
2. 说下301和302的区别？
3. 常用的异步请求处理方式？

题目一：如何对一数组进行去重，复杂度尽可能低些。

方法一：最简单的方法肯定是Set去重

function unique (arr) {
  return Array.from(new Set(arr))
}
var arr = [1,1,'true','true',true,true,15,15,false,false, undefined,undefined, null,null, NaN, NaN,'NaN', 0, 0, 'a', 'a',{},{}];
console.log(unique(arr))
 //[1, "true", true, 15, false, undefined, null, NaN, "NaN", 0, "a", {}, {}]

不考虑兼容性，这种去重的方法代码最少。这种方法还无法去掉“{}”空对象，后面的高阶方法会添加去掉重复“{}”的方法。

题目二：利用for循环嵌套，然后splice进行去重

function unique(arr){            
        for(var i=0; i<arr.length; i++){
            for(var j=i+1; j<arr.length; j++){
                if(arr[i]==arr[j]){         //第一个等同于第二个，splice方法删除第二个
                    arr.splice(j,1);
                    j--;
                }
            }
        }
return arr;
}
var arr = [1,1,'true','true',true,true,15,15,false,false, undefined,undefined, null,null, NaN, NaN,'NaN', 0, 0, 'a', 'a',{},{}];
console.log(unique(arr)) //[1, "true", 15, false, undefined, NaN, NaN, "NaN", "a", {…}, {…}]     //NaN和{}没有去重，两个null直接消失了

双层循环，外层循环元素，内层循环时比较值。值相同时，则删去这个值。

利用indexOf去重

function unique(arr) {
    if (!Array.isArray(arr)) {
        console.log('type error!')
        return
    }
    var array = [];
    for (var i = 0; i < arr.length; i++) {
        if (array .indexOf(arr[i]) === -1) {
            array .push(arr[i])
        }
    }
    return array;
}
var arr = [1,1,'true','true',true,true,15,15,false,false, undefined,undefined, null,null, NaN, NaN,'NaN', 0, 0, 'a', 'a',{},{}];
console.log(unique(arr))// [1, "true", true, 15, false, undefined, null, NaN, NaN, "NaN", 0, "a", {…}, {…}]  //NaN、{}没有去重

新建一个空的结果数组，for 循环原数组，判断结果数组是否存在当前元素，如果有相同的值则跳过，不相同则push进数组。

利用sort去重

function unique(arr) {
    if (!Array.isArray(arr)) {
        console.log('type error!')
        return;
    }
    arr = arr.sort()
    var arrry= [arr[0]];
    for (var i = 1; i < arr.length; i++) {
        if (arr[i] !== arr[i-1]) {
            arrry.push(arr[i]);
        }
    }
    return arrry;
}
     var arr = [1,1,'true','true',true,true,15,15,false,false, undefined,undefined, null,null, NaN, NaN,'NaN', 0, 0, 'a', 'a',{},{}];
        console.log(unique(arr))
// [0, 1, 15, "NaN", NaN, NaN, {…}, {…}, "a", false, null, true, "true", undefined]      //NaN、{}没有去重

利用sort()排序方法，然后根据排序后的结果进行遍历及相邻元素比对。

利用includes

function unique(arr) {
    if (!Array.isArray(arr)) {
        console.log('type error!')
        return
    }
    var array =[];
    for(var i = 0; i < arr.length; i++) {
            if( !array.includes( arr[i]) ) {//includes 检测数组是否有某个值
                    array.push(arr[i]);
              }
    }
    return array
}
var arr = [1,1,'true','true',true,true,15,15,false,false, undefined,undefined, null,null, NaN, NaN,'NaN', 0, 0, 'a', 'a',{},{}];
console.log(unique(arr))//[1, "true", true, 15, false, undefined, null, NaN, "NaN", 0, "a", {…}, {…}]     
//{}没有去重

题目二：如何判断一颗二叉树是不是对称二叉树。

• 对称二叉树:

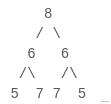
• 非对称二叉树:

对于二叉树遍历，有前序遍历、中序遍历、后序遍历3种常用的算法。

• 前序遍历：先遍历根节点，再遍历左右子树
• 中序遍历：先遍历左（右）子树，然后访问根节点，最后遍历右（左）子树
• 后序遍历：先遍历左右子树，再遍历根节点

在这里采用前序遍历的方法判断是否为对称二叉树：

var isSymmetric = function(root) {
    if(root == null){
        return true;
    }
    return isSym(root.left,root.right)
};
function isSym(left,right){
    if(left == null && right == null) {
        return true;
    }
    if(left == null || right == null){
        return false;
    }
    if(left.val != right.val){
        return false;
    }
    return arguments.callee(left.left,right.right) && arguments.callee(left.right,right.left);
}

题目三：数据扁平化处理

es6扁平化处理

let arr=[[1,2,3],4,5,[6,7,[8,9]]];
let bianping=arr=> arr.reduce((res,item)=> res.concat(Array.isArray(item)?bianping(item):item),[])
console.log(bianping(arr));

ES6加reduce加递归

let arr=[[1,2,3],4,5,[6,7,[8,9]]];
function bianping(arr){
    return arr.reduce((res,item) =>{
        return res.concat(Array.isArray(item)?bianping(item):item)
    },[])
}
console.log(bianping(arr));

递归

var arr=[[1,2,3],4,5,[6,7,[8,9]]];
function bianping(arr){
    var res=[];
    for(var i=0;i<arr.length;i++){
        var item=arr[i];
        if(Array.isArray(item)){
            console.log(item);
            res=res.concat(bianping(item));
        }else{
            res.push(item);
        }
    }
    return res;
}
console.log(bianping(arr));

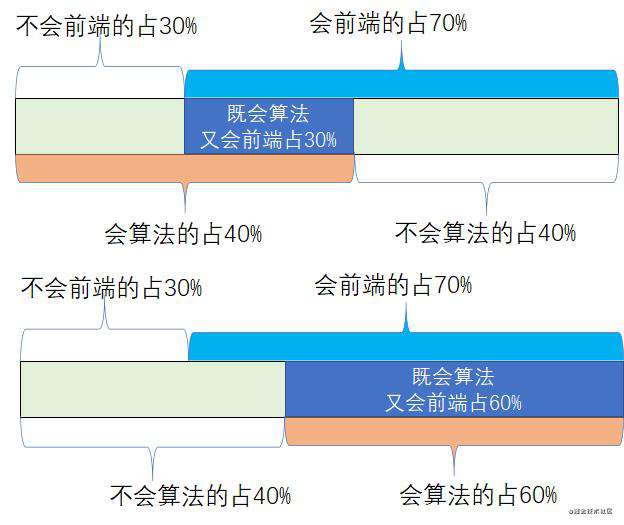
题目四：某公司会算法的占60%，会前端的占70%，会后端的占80%，求前端、后端、算法三者都会的人占多少范围？

分析：

• 先要分析出既会算法又会前端的所占比例
• 再计算当中既会算法又会前端后端的所占比例

第一步：计算得出既会前端又会算法的比例范围为30%-60%.

第二步：计算既会算法又会前端后端的所占比例范围为10%-60%

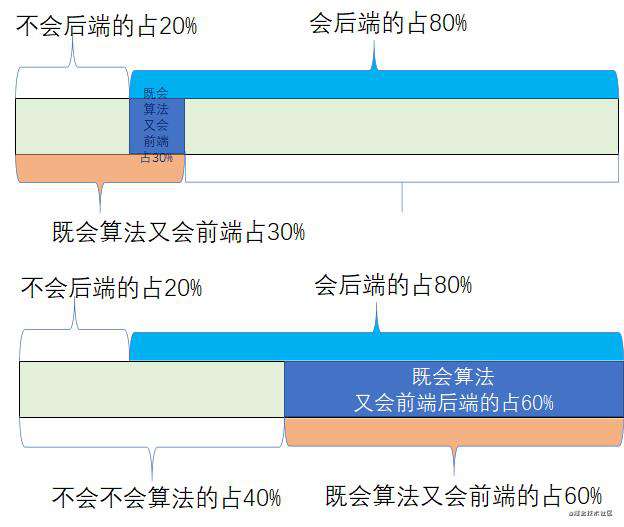
得到最后的比例为：10%-60%

以上是本次面试的所有题目与解答，如有出入，希望各位不吝赐教。