前言
以下内容介绍常见的排序算法,主要介绍算法的实现,算法的时间复杂度,排序算法是否稳定,并采用 Java Script 代码进行实现
算法稳定性
理论
算法是否稳定,是指排序过程中,当碰到两个元素相同时,是否会互换元素的位置,如果换则不稳定,如果不换则稳定;比如:a[i] 与 a[i + 1] 相等,却将 a[i + 1] 赋值给了 a[i],将 a[i] 赋值给了 a[i + 1]
应用
如果需要排序的是对象数组,其中 id、price、time 等属性,其中,默认使用 time 按递增序列排序,现在要使用 price 按递增序列进行重新排序,并且如果 price 相同,那么按 time 递增序列进行排序,因此可以理解为,如果 price 相同,不能改变相关元素的顺序,即需要使用稳定的排序算法
冒泡排序
思路
- 对数组进行遍历,比较相邻的两个元素,将大的放在后面
- 此方式进行一轮遍历后,数组的最后一个元素为数组中最大的数
- 因此,对上面的操作进行 n - 1 轮循环,将得到想要的结果
代码
var sortFun = function(arr){
let temp
for(let j = arr.length - 1; j > 0; j--){
for(let i = 0; i < arr.length - 1; i ++){
if(arr[i] > arr[i + 1]){
temp = arr[i]
arr[i] = arr[i + 1]
arr[i + 1] = temp
}
}
}
}
优化1
- 对上面的操作流程进行优化
- 第一次遍历 1 到 n,比较相邻的两个元素,将大的放在后面
- 通过以上的操作,则确定了最后一个元素为数组中最大的元素,因此第二次操作不需要参与遍历
- 因此第二次只需遍历 1 到 n - 1,比较相邻的两个元素,将大的放在后面
- 同理第三次只需遍历 1 到 n - 2,后面的可以依次类推,逐步减少
代码
var sortFun = function(arr){
let temp
for(let j = arr.length - 1; j > 0; j--){
for(let i = 0; i < j; i ++){
if(arr[i] > arr[i + 1]){
temp = arr[i]
arr[i] = arr[i + 1]
arr[i + 1] = temp
}
}
}
}
优化2
- 对上面的操作流程继续优化
- 增加变量 swap 标志,记录每一轮循环是否改变值,如果每改变,说明排序完成,后续操作为冗余,停止循环
var sortFun = function(arr){
let temp
let swap
for(let j = arr.length - 1; j > 0; j--){
swap = false
for(let i = 0; i < j; i ++){
if(arr[i] > arr[i + 1]){
temp = arr[i]
arr[i] = arr[i + 1]
arr[i + 1] = temp
swap = true
}
}
}
}
总结
- 以上实现的排序是稳定的,如果想要不稳定,只需将
arr[i] > arr[i + 1]改为arr[i] >= arr[i + 1] - 时间复杂度为 0(n^2)
- 优化后的算法,针对特殊数列复杂度会降低
选择排序
思路
- 遍历数组中未排序的元素,找出最小(大)值,放在第一个位置
- 重复第一步操作,直到所有元素均排序完毕
代码
var arraySort = function(arr){
let min
let temp
for(let i = 0; i < arr.length - 1; i++){
min = i;
for(let j = i + 1; j < arr.length; j++){
if(arr[min] > arr[j]){
min = j
}
}
if(min != i){
temp = arr[i];
arr[i] = arr[min]
arr[min] = temp
}
}
}
总结
- 最基本的实现为不稳定,如想实现稳定的选择排序或者了解选择排序的具体细节可阅读文章 《【JS算法】选择排序--稳定性》
- 时间复杂度为 0(n^2)
- 虽然选择排序的复杂度与冒泡排序相同,但对于普通的数据,选择排序的操作速度比冒泡排序快,因为选择排序中一次遍历结束后,才判断是否执行替换操作,而冒泡排序是每次都需要判断是否执行替换操作,因此冒泡排序中多了替换操作的负担。但是由于冒泡排序优化后,针对数据比较特殊的数列,可以降低复杂度,比如已经排好序的数列,使用优化后的冒泡排序复杂度为 0(n)。因此个人感觉没必要对这两种算法较真
插入排序
思路
- 此处以升序为例介绍
- 遍历待排序的数据
- 每次遍历中,取当前值向前查找与前面所有的值对比
- 如果被比较的值大于当前值,被比较的值向后移一位
- 如果被比较的值小于或等于当前值,停止查找,用当前值替换被比较的值
代码
var arraySort = function(arr){
let currentItem
let position
// 遍历数组
for(let i = 0; i < arr.length; i ++){
// 取当前值
currentItem = arr[i]
position = i
// 取当前值向前查找,如果查找完毕或者找到小于等于当前值的值,停止查找
while(position > 0 && arr[position - 1] > currentItem){
// 将查找的值后移
arr[position] = arr[position - 1]
position --
}
// 查找停止后,插入
arr[position] = currentItem
}
}
总结
- 以上实现的排序是稳定的,如果想要不稳定,只需将
arr[position - 1] > currentItem改为arr[position - 1] >= currentItem - 时间复杂度为 0(n^2)
- 与前两种算法相比,虽然时间复杂度同为 0(n^2)。但是将排序算法细分到数据比较次数和数据交换次数上,插入排序比前面的算法更具有优势,比如,无序度低的情况下,插入排序的操作次数将明显少于其他两种排序。同时它是稳定的排序。因此在工程中应用比较广泛
归并排序
合并函数
思路
- 传入原始数组,其中
start至mid为有序数列,mid + 1至end为有序数列 - 从原数组中根据
start和end浅拷贝出新数组tempArr - 用
leftPointer、rightPointer分别代表指向左右两个有序数列的指针 - 用
midPosition记录tempArr最中间的 key,从start到midPosition为第一个有序数列 - 用
endPosition记录tempArr最后面的 key,从midPosition + 1到endPosition为第二个有序数列 - 用
currentPointer指代原数组中,当前需要排序的位置 - 使用
leftPointer与rightPointer双指针遍历tempArr - 比较两个指针所指的数,将较小的数替换至原数组中
currentPointer所指的位置 - 如果
leftPointer > midPosition或rightPointer > endPosition则代表左序列或右序列已经全部插入,则只需将另一个序列剩余的数全替换至原数组中
代码
/**
* start -> mid 为有序数列
* mid + 1 -> end 为有序数列
* 此函数用于将 start -> mid 与 mid + 1 -> end 合并,组合成一个有序数列 start -> end
*/
var merge = function(arr, start, mid, end){
// 浅拷贝原数组
var tempArr = arr.slice(start, end + 1)
// tempArr 中左部分指针
let leftPointer = 0
// tempArr 中右部分指针
let rightPointer = mid + 1 - start
// mid 在 tempArr 中映射的位置
let midPosition = mid - start
// end 在 tempArr 中映射的位置
let endPosition = end - start
// 当前在排序的位置的指针
let currentPointer = start
while(currentPointer <= end){
// 左边排完,右边还没排完
if(leftPointer > midPosition){
arr[currentPointer] = tempArr[rightPointer]
rightPointer ++
}
// 右边排完,左边还没排完
else if(rightPointer > endPosition){
arr[currentPointer] = tempArr[leftPointer]
leftPointer ++
}
// 左边小于等于于右边
else if(tempArr[leftPointer] <= tempArr[rightPointer]){
arr[currentPointer] = tempArr[leftPointer]
leftPointer ++
}
// 左边大于右边
else{
arr[currentPointer] = tempArr[rightPointer]
rightPointer ++
}
currentPointer ++
}
}
递归实现
思路
-
采用递归的思路
-
使用二分法拆分数组,分为左右两个子数组
-
判断拆分好的子数组是否有序,默认情况下,子数组个数为 1 时认为是有序数组
-
如果是则不操作,如果不是则继续将当前数组拆分成左右两个子数组
-
递归的每一层拆分处理后,都可认为左右两个子数组是有序的,可以使用有序数列合并的方式进行合并
-
比如现在有未排序数组
[6,4,8,5]按以上思路进行排序 -
- 第零层
[6,4,8,5] - 第一层拆分成
[6,4]、[8,5] - 第二层拆分成
[6]、[4]、[8]、[5] - 由于第二层各自需要处理的数据都只有一个,所以不做多余操作,直接返回
- 回到第一层,调用合并函数,将
[6]、[4]合并,将[8]、[5]合并,最终得到[4,6]、[5,8] - 回到第零层,调用合并函数,将
[4,6]、[5,8]合并,最终得到[4,5,6,8]
- 第零层
代码
var arraySort = function(arr) {
const arrLength = arr.length
mergeSort(arr, 0, arrLength - 1)
}
var mergeSort = function(arr, start, end) {
if(start < end){
mid = Math.floor((start + end) / 2)
mergeSort(arr, start, mid)
mergeSort(arr, mid + 1, end)
// 优化代码,如果左序列最大值比右序列最小值小不用合并
if(arr[mid] < arr[mid+1]){
return
}
merge(arr, start, mid, end)
}
}
迭代实现
思路
- 使用双层循环,进行迭代操作
- 第一层控制参与合并的个数,循环变量 i
- 第二层表示参与合并数据开始位置的指针,循环变量 j
- 循环中调用合并函数,start = j,end = j + i - 1 || arr.length - 1,对数据进行两两合并
代码
var arraySort = function(arr) {
let end
let mid
for(let i = 2; i < arr.length * 2; i = i * 2){
for(let j = 0; j + i < arr.length + i; j = j + i){
end = j + i < arr.length ? j + i - 1 : arr.length - 1
mid = Math.floor((j + end)/2)
if(arr[mid] < arr[mid + 1]){
continue
}
merge(arr, j, Math.floor((j + end)/2), end)
}
}
}
总结
- 以上实现是稳定的,如果想要不稳定需要可以调整代码
- 当数据量小的时候,可以将序列近乎的认为是有序的,可以采用插入排序来微调,可以参照力扣官方的建议,在数据长度小于 15 的时候使用插入排序替代 merge 函数
- 进行 merge 操作的时候需要开辟空间,空间复杂度为 0(n),所以数据量大的时候容易耗内存
快速排序
例子理解可参考 www.cnblogs.com/MOBIN/p/468…
思路
- 用递归的思路实现
- 首先取数组中任意一个元素作为基数,此处取第一个,便于理解
- 然后遍历数组,比基数小的放左边,比基数大的放右边,与基数相等的可以任意放在左边或者右边,这样可以得到以基数为中心左右两个无序的数列,但是左边的都小于等于基数,右边的都大于等于基数
- 对左右两个无序序列再重复上面的操作,实现递归
代码
var arraySort = function(arr){
qSort(arr, 0, arr.length - 1)
}
var qSort = function(arr, start, end){
if(start >= end){
return
}
// 转换数据
let pivot = partition(arr, start, end)
// 将转化好的子数据再递归转换
qSort(arr, start, pivot - 1)
qSort(arr, pivot + 1, end)
}
/**
* 转换函数
* 取第一个值作为基数,遍历数组,将比基数小的放左边,大于等于基数的放右边
*/
var partition = function(arr, start, end){
// 基数取第一个元素
let pivot = arr[start]
// 如果 start 和 end 重合停止循环
while(start < end){
// 如果右指针指向的数比基数大,右指针左移
while(start < end && arr[end] >= pivot){
end --
}
// 上面的子循环结束,则代表右指针指向的数比基数小,将其放到 start 上
arr[start] = arr[end]
// 如果左指针指向的数比基数小,左指针右移
while(start < end && arr[start] <= pivot){
start ++
}
// 上面的子循环结束,则代表左指针指向的数比基数大,将其放到 end 上
arr[end] = arr[start]
}
arr[start] = pivot
return start
}
转换函数的另一种思路
/**
* 使用前后指针
* 前指针负责遍历数组
* 如果当前元素大于基数指针后移
* 如果当前元素小于基数,先将前指针指向的元素的后一位元素与后指针指向的元素互换,然后两个指针同时后移
* 以上操作能够实现,将前指针永远的拦在比基数大的元素前
* 比如有数组 [9,2,10,3,4], 那么如果后指针在 key = 3 的位置,前指针就在 key = 1 的位置
* 此时进行互换则得到 [9,2,3,10,4], 然后前指针后移到 key = 2 的位置,后指针后移到 key = 4 的位置,前指针依然被拦在比基数大的元素前
*/
var partition = function(arr, start, end){
let pivot = arr[start]
// 前指针
let jPointer = start
// 后指针
let iPointer = start + 1
// 如果 i 指针大于 end 结束循环
while(iPointer <= end){
// 如果后指针的值小于等于基数
if(arr[iPointer] <= pivot){
// 只有当需要互换的位置不同的时候才操作,避免不必要的操作
if(jPointer + 1 !== iPointer){
// 将前指针后面一位的值与后指针的值互换
let temp = arr[iPointer]
arr[iPointer] = arr[jPointer + 1]
arr[jPointer + 1] = temp
}
// 互换完成后,前指针后移
jPointer ++
}
// 后指针后移
iPointer ++
}
let temp1 = arr[start]
arr[start] = arr[jPointer]
arr[jPointer] = temp1
return jPointer
}
优化
- 当数列近乎有序的时,由于每次选取的都是第一个数,所以造成数列分割的极其不等,此时快排蜕化成O (n * n)的算法, 此时只要随机选取基准点即可
var partition = function(arr, start, end){
+ // start 到 end 中取随机值
+ let tempKey = arr[Math.floor(Math.random() * (end - start) + start)]
+ // 将随机值对应的元素与 start 对应的元素互换,达到基数随机的效果
+ let temp = arr[tempKey]
+ arr[tempKey] = arr[start]
+ arr[start] = temp
let pivot = arr[start]
// 前指针
let jPointer = start
// 后指针
let iPointer = start + 1
// 如果 i 指针大于 end 结束循环
while(iPointer <= end){
// 如果后指针的值小于等于基数
if(arr[iPointer] <= pivot){
// 只有当需要互换的位置不同的时候才操作,避免不必要的操作
if(jPointer + 1 !== iPointer){
// 将前指针后面一位的值与后指针的值互换
let temp = arr[iPointer]
arr[iPointer] = arr[jPointer + 1]
arr[jPointer + 1] = temp
}
// 互换完成后,前指针后移
jPointer ++
}
// 后指针后移
iPointer ++
}
let temp1 = arr[start]
arr[start] = arr[jPointer]
arr[jPointer] = temp1
return jPointer
}
-
当数列中包含大量的重复元素的时候,这一版的代码也会造成"分割不等“的问题,此时需要用三路快排来解决此问题。即小于基数的为一路,等于基数的为一路,大于基数的为一路
-
- 使用前、后、 尾三指针,用 i、j、k 表示
- start 位置存放基数
- start + 1 到 i(不包括 i )之间存放已确定比基数小的数
- i 到 j(不包括 j)之间存放已确定与基数相等的数
- k 指针,从最后一个元素开始向前遍历
- 如果 k 指针指向的元素比基数大,k 指针向前移动
- 如果 k 指针指向的元素比基数小
-
-
- k 指向的元素与 j 指向的元素互换
- 互换后 j 指针指向的元素比基数小,它应该放在 i 指针前面
- 所以需要将 i 指针指向的元素与 j 指针指向的元素互换
- 然后 i 指针和 j 指针都向后移动
- 因为从原来 j 位置换到 k 位置的元素还没有与基数对比,所以互换后 k 指针位置不变
- (这是我自己踩的大坑,做记录,可直接忽略)切记不能将 k指针指向的元素直接与 i 指针指向的元素先进行互换,再将 i 指针指向的元素与 j 指针指向的元素互换,因为指针变化过程中 k 指针可能与 j 指针重合,然后 i 指针在它们前面,如果使用此种交换方式将会等效于没互换
-
-
- 如果 k 指针指向的元素与基数相等
-
-
- k 指向的元素与 j 指向的元素互换
- j 指针向后移动
- 因为从原来 j 位置换到 k 位置的元素还没有与基数对比,所以互换后 k 指针位置不变
-
-
- 对于比基数小的数,如果 start 到 i 之间有无序数列,再针对此无序子序列递归调用以上方法
- 对于比基数大的数,如果 j 到 end 之间有无序数列,再针对此无序子序列递归调用以上方法
- 做优化也可以组合插入排序之类的排序方式,当无序数列长度小于等于 15 时直接调用插入排序进行微调
// 三路快排
var fun = function(arr, start, end) {
let pivot = arr[start]
// 前指针
let i = start + 1
// 后指针
let j = start + 1
// 尾指针
let k = end
while(k >= j){
if(arr[k] > pivot){
k --
}
else if(arr[k] < pivot){
// 因为 j 与 k 可能相等,一定要 k 先与 j 换,j 在与 i 换
swap(arr, k, j)
swap(arr, j, i)
i ++
j ++
}
else{
swap(arr, k, j)
j ++
}
}
swap(arr, start, i - 1)
if(i - start > 1){
fun(arr, start, i - 2)
}
if(end - j > 1){
fun(arr, j, end)
}
}
// 交换函数
var swap = function(arr, i, j){
// i j 相等时会出现 0 的bug
if(i === j){
return
}
arr[i] = arr[i] + arr[j]
arr[j] = arr[i] - arr[j]
arr[i] = arr[i] - arr[j]
}
堆排序
由于篇幅,此处没有列举 js 中堆实现的例子,可参考《【JS算法】堆排序》
堆
理论
堆,是具有下列性质的完全二叉树:每个节点的值都小于等于其左右孩子节点值是小根堆;(大于等于则是大根堆)。批注:有些参考书将堆直接定义为序列,但是,从逻辑结构上讲,还是将堆定义为完全二叉树更好。虽然堆的典型实现方法是数组,但从逻辑的角度上讲,堆实际上是一种树结构。
对于数组实现的堆,是一个完全二叉树,其中任意一个节点 i 都满足以下公式
- Parent(i) = floor((i-1)/2),i 的父节点下标
- Left(i) = 2i + 1,i 的左子节点下标
- Right(i) = 2(i + 1),i 的右子节点下标
思路
- 此思路用于将任意数组调整成大根堆
- 首先将数组想象成是一个完美二叉树
- 我们的目的是将这个二叉数调整成大根堆,即每个节点的值都大于等于其左右孩子节点值
- 首先,寻找到最后一个根节点,此根节点有一个孩子是数组的最后一个元素
- 然后找出大的孩子节点与根节点对比,如果大的孩子节点比根节点大,则将根节点与大的孩子节点互换,保证根节点最大
- 接着向前遍历根节点
- 对每个根节点,都首先找出比较大的孩子节点,然后将大的孩子节点与根节点对比
- 如果孩子节点比根节点大,那么将孩子节点与根节点互换
- 然后将互换后得到新值的孩子节点作为新的根节点,将其与它自己的子节点再重复以上对比,以此进行深度遍历的重复操作,直到此相关树上的根节点都比孩子节点大为止
- 深度遍历操作完后,继续执行前面的根节点遍历操作,直到遍历到最后一个根节点
代码
/**
* 此代码建议 mock 数据,并将其绘制成完美二叉树,参照二叉树进行阅读
*/
function buildHeap(data){
let len = data.length
// 从最后一个根节点开始,向前遍历所有根节点
// 取 len / 2 作为 i 的初始值,是因为最后一个孩子节点是 len - 1
// 它可能是左孩子也可能是右孩子,那么可以根据公式算出对应的根节点
// 它一定在 len / 2 附近,且小于 len / 2
for(let i = Math.floor(len / 2); i >= 0; i --){
heapAjust(data, i, len);
}
}
/**
* 根据传入的数据调整二叉树
* i 为根节点的 key
* len 为需调整数据的长度
*/
function heapAjust(data, i, len){
// 寻找 i 的左孩子
let child = 2 * i + 1
// 如果 child 大于 len 说明 i 不是根节点
while(child < len) {
// 比较两个孩子节点,将 child 指向大的那个
if(child + 1 <= len && data[child] < data[child + 1]){
child = child + 1
}
// 如果孩子节点比根节点大,两个节点互换
if(data[i] < data[child]){
let temp = data[i]
data[i] = data[child]
data[child] = temp
// 互换之后将被更新的孩子节点继续作为根节点,进行深度查找
i = child
child = 2 * i + 1
}
else {
break
}
}
}
堆排序
思路
- 先将整个数组调整成大根堆
- 则数组的第一个元素最大,将其与数组最后一个元素替换,此时大根堆被破坏
- 重新调整前 length - 1 个元素,将它们调整成新的大根堆
- 以此循环,直到堆中的元素只有一个时
代码
var arraySort = function(arr) {
// 将数组调整成大根堆
buildHeap(arr);
// 下面需要注意的时候参数的边界
for(let i = arr.length - 1; i >= 0; i --) {
// 互换数据
let temp = arr[i]
arr[i] = arr[0]
arr[0] = temp
// 将前面的元素重新调整成大根堆
heapAjust(arr, 0, i-1);
}
}
总结
- 堆排序是不稳定的
- 在寻找前几个值最大的场景中比较好用
希尔排序
思路
- 希尔排序是插入排序的优化版本
- 任意选择一个从 1 开始的递增序列,最大值小于需排序数据的长度,此处用递增数列 1,2,4 .... arr.length / 2 举例子
- 从上面确定的数列中,从最大值开始取元素,将每个取出的元素作为间隔大小
- 以间隔为初始元素位置,比如间隔为 2 则首元素为 2,逐个向后遍历
- 遍历过程中,将每个元素与前面的元素进行比较,以插入排序的思路,插入到合适的位置
- 向前选择前面的元素并不是每个元素都选,而是以当前元素所在位置为参照点,以间隔为分隔进行选择,形成跨元素比对
- 比如 [2,3,1,9],当前间隔为 2,当前元素为 1,key = 2,那么向前选择比较元素,直接选 2,key = 0
代码
/**
* 排序
*/
var arraySort = function(arr){
// 控制间隔
for(let delta = Math.floor(arr.length / 2); delta >= 1; delta = Math.floor(delta / 2)){
// 从第一个间隔距离开始向后逐个遍历
for(let i = delta; i < arr.length; i ++){
// 每个元素,向前以间隔为距离实现跨间隔的插入排序
for(let j = i; j >= delta && arr[j] < arr[j - delta]; j = j - delta){
swap(arr, j, j - delta)
}
}
}
}
/**
* 互换元素
*/
var swap = function(arr, i, j){
if(i === j){
return
}
arr[i] = arr[i] + arr[j]
arr[j] = arr[i] - arr[j]
arr[i] = arr[i] - arr[j]
}
总结
- 以上使用的增量是最初Donald Shell提出的增量,即折半降低直到1。据研究,使用希尔增量,其时间复杂度还是O(n2)
- 可以使用优化的增量 Hibbard:{1, 3, ..., 2k-1} 该增量序列的时间复杂度大约是O(n1.5)
var arraySort = function(arr){
+ let delta = 1
+ while(delta < arr.length / 3){
+ delta = delta * 3 + 1
+ }
+ for(; delta >= 1; delta = Math.floor(delta / 3)){
- for(let delta = Math.floor(arr.length / 2); delta >= 1; delta = Math.floor(delta / 2)){
for(let i = delta; i < arr.length; i ++){
for(let j = i; j >= delta && arr[j] < arr[j - delta]; j = j - delta){
swap(arr, j, j - delta)
}
}
console.log(arr)
}
}
计数排序
思路
- 找出待排序的数组中最大和最小的元素
- 统计数组中每个值为 i 的元素出现的次数,存入数组 C 的第 i 项
- 对所有的计数累加(从 C 中的第一个元素开始,每一项和前一项相加)
- 反向填充目标数组:将每个元素i放在新数组的第 C(i) 项,每放一个元素就将 C(i) 减去 1
代码
var arraySort = function(arr, arrMax, arrMin){
let b = []
let count = new Array(arrMax - arrMin + 1).fill(0)
for(let i = 0; i < arr.length; i ++){
// 将 value 与 count 中的 key 做映射
count[arr[i] - arrMin] ++
}
for(let i = 0; i < count.length; i ++){
// 遍历 count 使用 count 的元素创建数组,key 作为数组的中填充的值,value 作为数组的个数
b = b.concat(new Array(count[i]).fill( i + arrMin))
}
Object.assign(arr, b)
}
var arr = [99,33,0,34,64,22,45,45,77,55,66,55]
arraySort(arr, 99, 0)
// [0, 22, 33, 34, 45, 45, 55, 55, 64, 66, 77, 99]
总结
- 由于此算法的局限性,它只能用于简单数组的排序,因此研究此算法的稳定性没有意义,但仔细深究,它是稳定的
- 针对数据范围较小的数组,比如学生成绩,可用此方式进行排序
最后
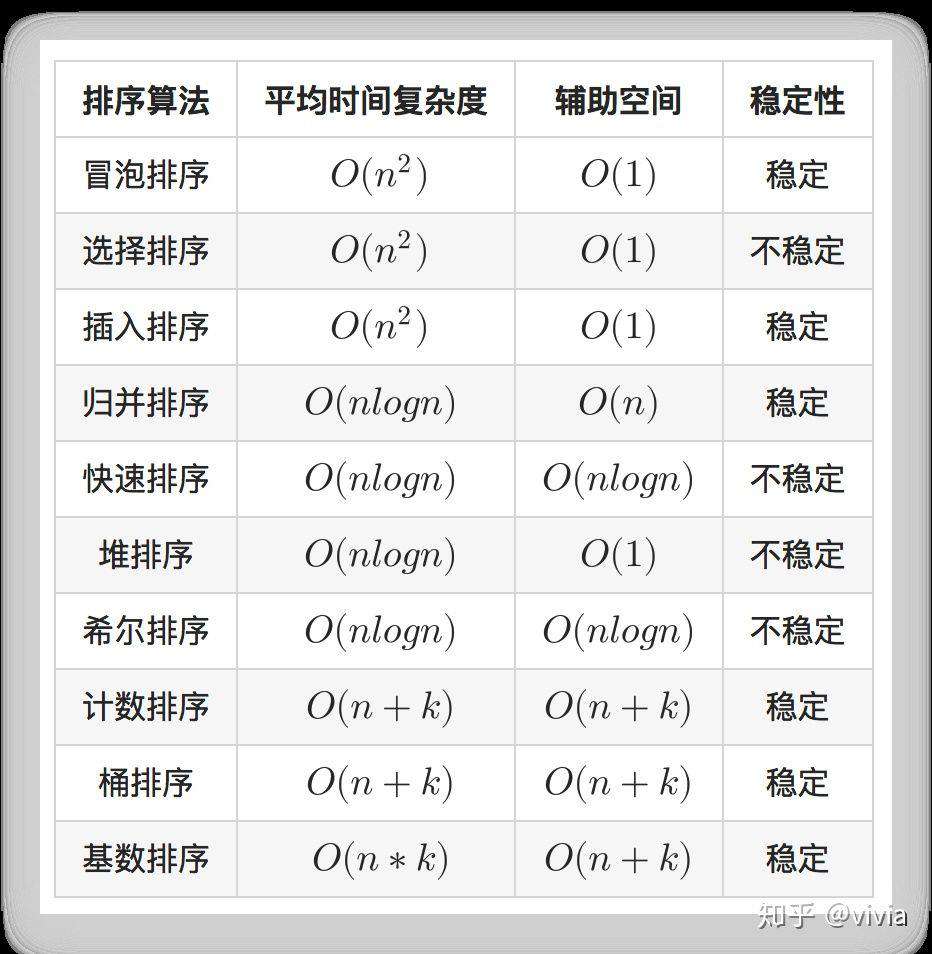
- 此文章参考[《算法总结] 十大排序算法》和 《面试 | 常用的排序算法总结》,没有罗列基数排序和桶排序,个人感觉这两种排序太过冷门,使用场景太少
- 偷一张[《算法总结] 十大排序算法》中复杂度和稳定性总结的图
常见问题FAQ
- 免费下载或者VIP会员专享资源能否直接商用?
- 本站所有资源版权均属于原作者所有,这里所提供资源均只能用于参考学习用,请勿直接商用。若由于商用引起版权纠纷,一切责任均由使用者承担。更多说明请参考 VIP介绍。
- 提示下载完但解压或打开不了?
- 找不到素材资源介绍文章里的示例图片?
- 模板不会安装或需要功能定制以及二次开发?




发表评论
还没有评论,快来抢沙发吧!